1552. Быстрый почтальон
Почтальону
необходимо разнести несколько писем по домам, расположенным на одной улице. У
него имеются адреса (в виде расстояния в метрах от левого края улицы до места
доставки письма) и максимальное время для каждого письма, за которое его нужно
доставить. Скорость почтальона
Вход. Содержат несколько тестов, каждый из которых состоит из
трех строк. Первая строка каждого теста содержит два числа: количество адресов AddrNum (1 ≤ AddrNum ≤ 50) и начальное положение почтальона initialPos (1 ≤ initialPos ≤ 106) в том
же формате что и адреса. Вторая и третья строка содержит AddrNum чисел. i-ый
элемент второй и третьей строки представляет собой адрес и максимальное
допустимое время доставки i-ого
письма. Каждое число во второй строке лежит в промежутке от 1 до 106
включительно. Каждое число в третьей строке находится в пределах от 1 до 109
включительно.
Выход. Для каждого теста в отдельной строке вывести наименьшее
возможное время доставки всех писем при заданных ограничениях или -1 если этого
совершить невозможно.
|
Пример
входа |
Пример
выхода |
|
4 4 1 3 5 7 9 2 5 100 4 2 1 7 10 4 15 6 28 39 |
13 20 |
РЕШЕНИЕ
динамическое программирование
Анализ алгоритма
Если почтальон
на своем пути поравняется с некоторым домом, куда следует доставить письмо, то
его следует отдавать сразу же, при первом же подходе к дому. Если почтальон уже
разнес письма в i - ый и j - ый дома, то он точно уже разнес
письма во все дома, которые находятся между i
- ым и j - ым домом. Таким образом,
множество домов, куда уже разнесена почта, представляет собой отрезок прямой с
точкой initialPos внутри. Следует
также отметить, что направление движения почтальон может менять только в точке
с домом, в который он только что доставил письмо.
Состояние
почтальона определим тройкой чисел:
1. левый конец
интервала домов, куда уже разнесена почта;
2. правый конец
интервала домов, куда уже разнесена почта;
3. текущее
положение почтальона;
Вместо самих
чисел в состоянии почтальона лучше хранить их индексы в массиве address. На каждом шаге (i, j,
k) следует определить, куда лучше
двигаться почтальону: вправо (i, j + 1, j + 1) или влево (i – 1, j,
i – 1). Также заметим, что для каждого состояния (i, j, k) текущее положение почтальона k равно i или j.
В ячейках sol[i][j][0]
будем хранить наименьшее время, за которое почтальон разнесет все письма в дома
в интервале (i, j), причем находиться будет в точке i (в левом конце интервала). Соответственно в sol[i][j][1]
будет содержаться та же информация, только почтальон будет находиться в правом
конце интервала – в точке j.
Отсортируем
адреса домов по возрастанию их координат. Чтобы при сортировке соответствующим
образом переставлялось и граничное время доставки, создадим вектор пар houses,
первый элемент которого содержит адрес дома, а второй – максимальное время
доставки письма в этот дом. При сортировке вектора пар по возрастанию
сортировка производится по первой компоненте – то есть по расстоянию от левого
края улицы.
Инициализация
массива sol:
sol[i][i][0]
= sol[i][i][1] = | address[i] – initialPos | = | houses[i].first – initialPos |
Для доставки
письма в единственный дом, индекс которого равен i, необходимо затратить время, равное расстоянию от начального
положения initialPos до
местоположения дома address[i].
Рассмотрим интервал
(i, j). Почтальон может оказаться в его левом конце, двигаясь либо с
левого конца интервала (i + 1, j), либо с правого конца интервала (i + 1, j). В первом случае ему требуется пройти расстояние address[i + 1] – address[i], во втором address[j] –
address[i]. То есть
sol[i][j][0]
= min(sol[i + 1][j][0] + address[i + 1] –
address[i],
sol[i + 1][j][1] + address[j] –
address[i])
Аналогично
почтальон может оказаться в правом конце итервала (i, j), если он будет
двигаться либо с левого конца интервала (i,
j – 1), либо с правого конца
интервала (i, j – 1). В первом случае ему требуется пройти расстояние address[j] –
address[i], во втором address[j]
– address[j – 1]. Таким образом
sol[i][j][1]
= min(sol[i][ j – 1][0] + address[j] –
address[i],
sol[i][
j – 1][1] + address[j] –
address[j – 1])
Если на
каком-нибудь этапе вычисления значение sol[i][j][0] (или sol[i][j][1]) станет большим
maxTime[i] (или соответственно
maxTime[j]), то установим его равным
плюс бесконечности (значению INF = 2000000000). Последнее означает тот факт,
что добраться до соответствующего дома в отведенное время почтальон не может.
Почтальон
доставит все письма, когда будут пройдены все дома из интервала (0, n – 1), где n – количество домов. При этом нам не важно, в каком из концов
этого интервала закончит путь почтальон. То есть ответом будет значение
min(sol[0][n – 1 ][0], sol[0][n – 1][1])
Если это
значение равно плюс бесконечности, то разнести письма в срок не удастся и
следует вернуть -1 как требуется в условии задачи.
Пример
Рассмотрим
первый тест. Красным отображен весь путь почтальона.
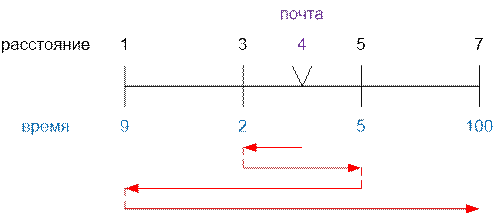
Рассмотрим
значения sol для интервала [3; 5].
·
В точку 3 можно попасть по пути 4 → 5 → 3, sol[3][5][0] =
1 + 2 = 3;
·
В точку 5 можно попасть по пути 4 → 3 → 5, sol[3][5][1] =
1 + 2 = 3;
Однако поскольку
имеется ограничение по времени на доставку в точку 3 (не более 2 секунд), то
будет установлено sol[3][5][0] = +∞.
Рассмотрим
значения sol для интервала [1; 5].
·
Двигаться в 1 из 3 мы не можем, так как sol[3][5][0] = +∞. Поэтому
попасть в 1 можно только из правого конца интервала [3; 5]:
sol[1][5][0] = sol[3][5][1] + |5 – 1| = 3 + 4 = 7;
·
Попасть в правый конец интервала [1; 5] можно только из
концов интервала [1; 3]:
sol[1][5][1] = min(sol[1][3][0] + |5 –
1|, sol[1][3][1] + |5 – 3|) =
min(3 + |5 – 1|, 5 + |5 – 3|)
= min(7, 7) = 7
Из-за ограничения
по времени доставки в точку 5 (не более 5 секунд) будет установлено sol[1][5][1] = +∞.
Реализация алгоритма
Объявим
необходимые массивы и переменные.
int sol[50][50][2];
int i, res, Num, value, InitPos;
vector<int>
address, maxTime;
Функция minTime возвращает наименьшее возможное
время доставки всех писем при заданных ограничениях.
int minTime(void)
{
int res, i, j, n = address.size();
Создаем массив пар houses, содержащий адреса и время доставки
писем. Сортируем пары по адресам.
vector<pair<int,int> > houses;
for(i = 0; i < n; i++)
houses.push_back(make_pair(address[i],maxTime[i]));
sort(houses.begin(),houses.end());
Инициализируем
массив sol.
memset(sol,0,sizeof(sol));
for(i = 0; i < n; i++)
{
sol[i][i][0] = sol[i][i][1] = abs(houses[i].first - InitPos);
if (sol[i][i][0] > houses[i].second)
sol[i][i][0] = sol[i][i][1] = INF;
}
Заполняем ячейки массива sol.
for(i = n - 1; i >= 0; i--)
for(j = i + 1; j < n; j++)
{
sol[i][j][0] = min(sol[i+1][j][0] + houses[i+1].first –
houses[i].first, sol[i+1][j][1] + houses[j].first - houses[i].first);
if (sol[i][j][0] > houses[i].second)
sol[i][j][0] = INF;
sol[i][j][1] = min(sol[i][j-1][0] + houses[j].first –houses[i].first,
sol[i][j-1][1] + houses[j].first - houses[j-1].first);
if (sol[i][j][1] > houses[j].second)
sol[i][j][1] = INF;
}
Вычисляем ответ.
res = min(sol[0][n-1][0],sol[0][n-1][1]);
if (res == INF) return
-1;
return res;
}
Основная часть программы.
while(scanf("%d %d",&Num,&InitPos)
== 2)
{
address.clear(); maxTime.clear();
for(i = 0; i < Num; i++)
scanf("%d",&value),address.push_back(value);
for(i = 0; i < Num; i++)
scanf("%d",&value),maxTime.push_back(value);
res = minTime();
printf("%d\n",res);
}